2. Extremal Graph Theory

An interesting question that mathematicians are curious about is the maximum number of edges in a n-vertex graph \(G\) that forbids some other graph \(H\). In other words, \(G\) cannot contain \(H\) as a subgraph.

Mantel's Theorem

We may also start from the simplest question, what is the maximum number of edges in a n-vertex graph without any triangle? This is a foundational problem in extremal graph theory, where people study how the global properties of a graph influence local substructure.

Hint: Try solving the case when \(n=3,4,5\). Do you see any pattern?

(Mantel's Theorem): \(K_{\lfloor n/2\rfloor,\lceil n/2\rceil}\) has the most number of edges among all triangle-free graphs. So every \(n\)-vertex triangle-free graph has at most \(\lfloor n^2/4\rfloor\) edges.

We will give two different proofs of Mantel's theorem and each illustrates a different technique in combinatorics. The proof requires some knowledge of Cauchy-Schwarz Inequality, which states that for any two list of real numbers \(a_1,a_2,\dots,a_n\) and \(b_1,b_2,\dots,b_n\), we have:

\[ (a_1^2+a_2^2+\cdots+a_n^2)(b_1^2+b_2^2+\cdots+b_n^2)\ge(a_1b_1+a_2b_2+\cdots+a_nb_n)^2 \]

It has many proofs but I will not show them here since it's unrelated to our topics. Feel free to read one of my previous blog post on Olympiad Inequalities, in which I discuss more about these inequalities.

First Proof of Mantel's Theorem: Let \(G=(V,E)\) be a triangle-free graph with \(n\) vertices and \(m\) edges. For any edge \((x,y)\) in the graph, by the triangle-free condition, \(x\) and \(y\) don't have common neighbors, otherwise suppose \(z\) is the neighbor of \(x\) and \(y\), \(x,y,z\) will form a triangle.

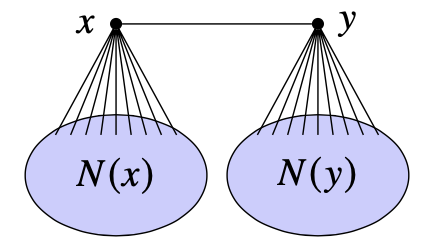
Thus, we have \(\deg x + \deg y\le n\). Go through all the edges of \(G\) and sum this up, we get: $$\sum_{(x,y)\in E}(\deg x + \deg y)\le \sum_{(x,y)\in E}n=mn$$

On the other hand, for each vertex \(x\), the term \(\deg x\) appears for every edge \((x,y)\) in \(E\) in the above inequality. Thus, in total \(\deg x\) appears \(\deg x\) times:

\[\sum_{(x,y)\in E}(\deg x + \deg y)=\sum_{x\in V}(\deg x)^2\le mn\]

However, by Cauchy-Schwarz inequality we can also get:

\[ n\sum_{x\in V}(\deg x) ^2 =(1+1+\cdots + 1)\sum_{x\in V}(\deg x) ^2\ge (\sum_{x\in V}\deg x)^2=(2m)^2 \]

Combine the above two inequalities,

\[ (2m)^2/n\le mn\implies m\le n^2/4 \]

as desired.

Second Proof of Mantel's Theorem: Let \(v\) be a vertex of maximum degree in the graph \(G\). For any \(x,y\) in the neighborhood \(N(v)\) of \(v\), \(x\) and \(y\) are not adjacent by the triangle-free condition.

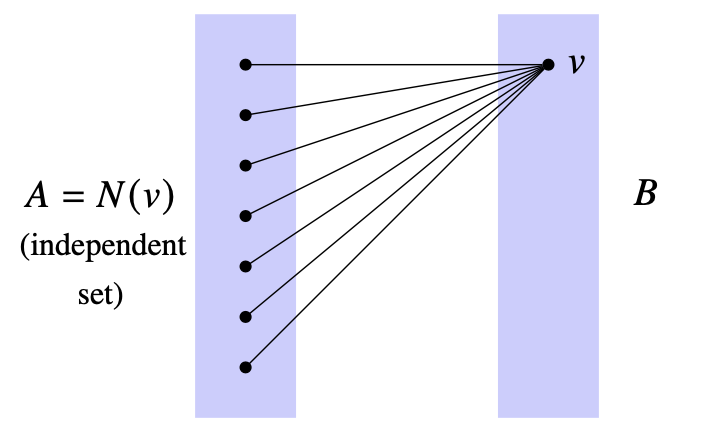
Let \(A=N(v),B=V\setminus A\). All the edges in \(G\) have an endpoint in \(B\) (because the two vertices of the edge cannot be both in \(A\)). By this relation, we have the following inequality:

\[ m\le \sum_{x\in B}\deg x\le |B|\max_{x\in V}\deg x \le |B||N(v)|\le (\dfrac{|A|+|B|}{2})^2= \dfrac{n^2}{4} \]

where the last \(\le\) sign is derived by AM-GM inequality.

Exercise: Can you prove Mantel's theorem by induction?

Proof: I will show the induction proof when \(n\) is even, so \(n=2k\). The odd case works similarly and is left to the readers.

When \(k=1\), every graph with two vertices has at most \(1\) edge so the claim holds.

For \(k > 1\), we can pick an edge \((x,y)\) in the graph and let \(G'\) denote the subgraph using the other vertices.

• if \(G'\) has more than \((k-1)^2\) edges, then \(G'\) is not triangle-free by induction.

• Otherwise, for any vertex \(v\) in \(G'\), we cannot have \((x,v)\) and \((y,v)\) both in our graph by triangle-free condition. So the total number of edges in \(G\) is at most

  \[(k-1)^2+2(k-1)+1=k^2-2k+1+2k-2+1=k^2\]

Thus the claim holds for all even \(n\).

Exercise: Prove that a graph with \(n\) vertices and \(m\) edges has at least

\[ \dfrac{4m}{3n}(m-\dfrac{n^2}{4})\quad\text{triangles} \]

Hint: We can count the number of triangles by the same method as what we did in the first proof.

Proof: The number of triangles with the edge \((x,y)\) is at least \(\deg x + \deg y - n\). If we count this way, every triangle is counted three times since it has three edges. Thus, the lower bound of the number of triangles is:

\[ \frac 13\sum_{(x,y)\in E}(\deg x + \deg y-n)=\frac13\bigg(\sum_{x\in V}(\deg x)^2-mn\bigg) \]

Apply Cauchy-Schwarz inequality and we get:

\[ \frac13\bigg(\sum_{x\in V}(\deg x)^2-mn\bigg)\ge \frac{1}{3n}\bigg(\sum_{x\in V}\deg x\bigg)^2-\frac{mn}{3}=\frac{4m^2}{3n}-\frac{mn}{3}=\frac{4m}{3n}(m-\frac{n^2}{4}) \]

Turán's Theorem

Turán's theorem is the generalization of Mantel's theorem from triangles to larger cliques. It provides the answer to this question:

What is the maximum number of edges in a \(K_{r+1}\)-free graph on \(n\) vertices?

Note that for \(r=2\) our answer is Mantel's theorem and the graph we have is a bipartite graph with two parts with sizes as close as possible. It feels natural for us to hypothesize that:

We call the complete \(r\)-partite graph with its \(n\) vertices distributed among its \(r\) parts as evenly as possible \(T_{n,r}\), also known as the Turán's graph. More formally, for \(n = ra+b,0\le b<r\), and \(a,b\) are integers, we have \(b\) parts with size \(a+1\) and \(r-b\) parts with size \(a\) in \(T_{n,r}\). Below is an example of \(T_{13,4}\):

Turán's theorem: The Turan's graph \(T_{n,r}\) is the unique \(n\)-vertex graph that maximizes the number of edges among all \(K_{r+1}\)-free graphs.

Exercise: Assume that we have proven Turán's theorem. Prove that

\[ e(T_{n,r})\le(1-\dfrac1r)\dfrac{n^2}2 \]

where \(e(G)\) denotes the number of edges in a graph \(G\) and we have equality if and only if \(n\) is divisible by \(r\).

Hint: We can use AM-GM to prove this, notice that \(n\) won't be divided in \(r\) equal parts when \(n\) is not divisible by \(r\).

Lemma: \(T_{n,r}\) is the unique \(n\)-vertex \(r\)-partite graph with the maximum number of edges.

Hint 1: We can prove by contradiction! Let's say we have a \(n\)-vertex \(r\)-partite graph with the maximum number of edges that is not \(T_{n,r}\), how can we adjust it to increase the number of edges?

Hint 2: For \(b-a\ge 2\), we have

\[ (a+1)(b-1)=ab+(b-a-1)>ab \]

Proof: Suppose we have a \(n\)-vertex \(r\)-partite graph with the maximum number of edges. Then it should be a complete \(r\)-partite graph, otherwise we can add edges between its different parts.

For any two vertex parts \(A\) and \(B\), if \(|B|-|A|\ge 2\) we can apply the inequality in the previous hint and see it's better to move an vertex of \(B\) to \(A\). Thus, all \(r\) parts must have sizes within one of each other.

There are also many proofs for Turán's theorem. We will focus on a proof that is extended from our previous proof of Mantel's theorem. Mathematical induction plays an important role in this proof and other proofs!

First proof of Turán's theorem: We prove by induction on \(r\). When \(r=1\), this is trivial since a \(K_2\)-free graph is empty. Now assume that the theorem holds for every \(n\) for \(r-1\).

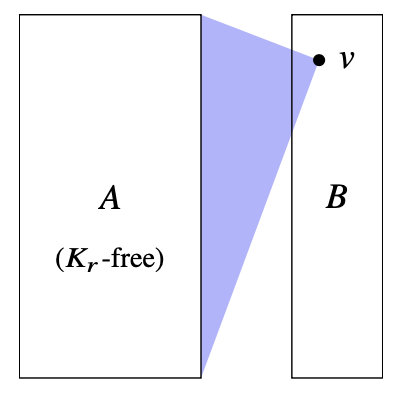
Let \(G\) be a \(K_{r+1}\)-free graph and \(v\) a vertex of maximum degree in \(G\). The neighborhood of \(v\) \(A=N(v)\) is \(K_r\)-free. By induction, we know that

\[ e(A)\le e(T_{|A|,r-1}) \]

Let \(B=V\setminus A\). Since \(v\) is a vertex of maximum degree, we have \(\deg x\le \deg v = |A|\) for all \(x\in V\). The number of edges with at least one vertex in \(B\) is:

\[ e(A,B) + e(B)\le \sum_{x\in B}\deg x \le |B|\max_{x\in B}\deg x\le |A||B| \]

Thus

\[ e(G)=e(A) + e(A,B) + e(B)\le e(T_{|A|,r-1}) + |A||B|\le e(T_{n,r}) \]

the final equality follows from that \(e(T_{|A|,r-1}) + |A||B|\) is the number of edges in a \(r\)-partite graph with \(n\) vertices and our previous lemma.

What we are curious about in this chapter is generally how big an \(n\)-vertex \(H\)-free graph \(G\) can be. Thus, we develop a notation \(ex(n,H)\) as the maximum number of edges in \(G\). We are curious about how \(ex(n,H)\) grows as \(n\to \infty\), which leads to extremal graph theory.

Problems

Every graph \(G\) with average degree \(d\) contains a subgraph \(H\) such that all vertices of \(H\) has degrees at least \(d/2\).

Hint: Delete the vertices with degree less than \(d/2\) until the graph meets our condition. Why does this guarantee a solution?

Prove Turán's theorem by induction on \(n\).

Hint: For an \(n\)-vertex \(K_{r+1}\)-free graph \(G\) with the maximum number of edges, \(G\) contains \(K_r\) as a subgraph. Let \(A\) be the vertex set of a \(K_r\) in \(G\) and \(B=V\setminus A\).

(KST Theorem) For positive integers \(s\le t\), there exist some constant \(C\) such that for all \(n\):

\[ ex(n,K_{s,t})\le Cn^{2-1/s} \]

Hint: Let \(X\) be the number of \(K_{s,1}\) in \(G\). Count \(X\) in two different ways to show that:

\[ X=\sum_{x\in V}\binom{\deg x}{s}\le \binom{n}{s}(t-1) \]

(IMO 1992/3): Consider \(9\) points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of \(n\) such that whenever exactly \(n\) edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.

Hint 1: Rephrase it in the language of graph theory and make connections to the theorems we have learned.

Hint 2: Apply Turán's Theorem and Ramsey's number \(R(3,3)=6\).

Let \(T\) be a tree with \(t\) edges. Prove that every graph \(G\) with average degree at least \(2t\) contains \(t\) as a subgraph.