F=ma Guide

The syllabus is inspired by the video F=ma Complete Guide. First, there are some helpful things to know about before taking the F=ma exam:

• 75 minutes, 25 questions
• Calculators are allowed
• 5 choices per question
• 1 point per correct question, no penalty for guessing.
• Score 14-18 to qualify for USAPhO
• 400 out of 6000 qualify
• Average score = 8/25

Math

Below are some math prerequisites ranked based on their importance in F=ma:

Vectors

Vectors are very important math tools in physics. We can see most of the physical quantities, like force, displacement, velocity, etc., as vectors.

• Vector addition: \((x_1,y_1,z_1)+(x_2,y_2,z_2)=(x_1+x_2,y_1+y_2,z_1+z_2)\)
• Magnitude of a vector satisfies Pythagorean theorem, so for \(v_1=(x_1,y_1,z_1)\), \(|v_1|=\sqrt{x_1^2+y_1^2+z_1^2}\)
• We can express a 2D-vector as its magnitude and its direction.
• Dot product: \((x_1,y_1,z_1)\cdot (x_2,y_2,z_2)=x_1x_2+y_1y_2+z_1z_2\), it also satisfies distributivity, so that \(a\cdot (b+c)=a\cdot b + a\cdot c\)
• \(v_1\cdot v_2=|v_1||v_2|\cos\theta\), where \(\theta\) is the angle between to vectors.
• Cross product: \((x_1,y_1,z_1)\times (x_2,y_2,z_2)=(y_1z_2-y_2z_1,z_1x_2-z_2x_1,x_1y_2-x_2y_1)\)
• \(|v_1\times v_2|=|v_1||v_2|\sin\theta\)

Trigonometry

• \(\sin(\alpha\pm \beta) =\sin\alpha\cos\beta\pm\cos\alpha\sin\beta\)
• \(\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta\)
• \(\tan(\alpha\pm\beta)=\dfrac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}\)

Basic Calculus

You don't need to know this to solve 95% of F=ma problems, but it could be helpful in some problems:

• \((x^n)'= nx^{n-1},(\sin x)'=-\cos x,(\cos x)'=\sin x,(e^x)'=e^x,(\ln x)'=1/x\)
• \((f+g)'=f'+g'\)
• \((f\cdot g)'=f\cdot g'+f'\cdot g\)
• \((f/g)'=(f'\cdot g-g'\cdot f)/g^2\)
• \(f(g(x))'=f'(g(x))\times g'(x)\) or simply \(\dfrac{dy}{dx}=\dfrac{dy}{du}\dfrac{du}{dx}\)

Taylor series

\[ F(x)=F(x_0)+\sum F^{(n)}(x_0)(x-x_0)^n/n! \]

In cases when \(x-x_0\ll 1\), we can take linear approximation:

\[ F(x)=F(x_0)+F'(x_0)(x-x_0) \]

Some useful examples:

\[\sin x= x,\cos x = 1-x^2/2,e^x=1+x,\ln(1+x)=x,(1+x)^n=1+nx\]

Dimensional Analysis

Dimensional Analysis is very useful in both physics and engineering. It is the analysis of the relationships between different physical quantities (e.g acceleration, pressure, velocity, force) by identifying their base quantities (e.g. length, mass, time) and their units (meters, kilograms, seconds). It is important to remember how units are related through formulas!

For example, in kinematics, we use the equations of motion to describe the motion of an object. One of the equations is:

\[ x = x_0 + v_0t + (1/2)at^2 \]

Where \(x\) is the final position of the object, \(x_0\) is the initial position, \(v_0\) is the initial velocity, \(t\) is the time, and \(a\) is the acceleration.

We can use dimensional analysis to check that the units of the different terms in the equation are consistent. The units of \(x\), \(x_0\) are length (e.g. meters), the unit of \(v_0\) is length over time (e.g. meters per seconds), the units of \(t\) is time (e.g. seconds), and the units of \(a\) are length per time squared (e.g. meters per second squared).

So we can check that the equation is dimensionally consistent by making sure that the units on both sides of the equation are the same. $$[L] = [L] + [L/T]\times[T] + (1/2)[L/T^2]\times[T^2]$$ On both sides of the equation, we have length units, which means that the equation is dimensionally consistent and it's a correct equation of motion.

Error Propagation

In statistics, propagation of uncertainty (or propagation of error) is the effect of variables' uncertainties on the uncertainty of a function based on them.

The uncertainty u can be expressed in a number of ways. e.g. the absolute error \(\delta x\) , the relative error \(\delta x/x\).

If \(x\) has uncertainty (error) \(\delta x\) , then \(cx\) has uncertainty \(c\delta x\) .

If \(x\) and \(y\) have independent random errors \(\delta x\) and \(\delta y\) , then the error in \(z=x+y\) is

\[ \delta z=\sqrt{\delta x^2+\delta y^2} \]

the error in \(z=x\times y\) or \(z=x/y\) is:

\[ \frac{\delta z}{z}=\sqrt{(\frac{\delta x}{x})^2+(\frac{\delta y}{y})^2} \]

If \(z=f(x)\) for some function \(f\), then

\[ \delta z=|f'(x)|\delta x \]

Thus, \(x^n\) has relative uncertainty:

\[ \delta(x^n)/x^n=|n|\delta x/x \]

Practice problems: 2018AP12,2018AP25,2019AP11,2019AP16,2019BP18,2021P8,2020AP23,2020BP25

Challenge problem:2019BP25

Kinematics

All formulas in kinematics is essentially just:

\[ v=\dfrac{dx}{dt},a=\dfrac{dv}{dt}=\dfrac{d^2x}{dt^2} \]

If you have some knowledge of calculus, then you don't even need to memorize any other formulas! But I will still put some useful formulas in constant acceleration motion below:

• The relationship between initial and final velocity: \(v_f=v_0+at,v_f^2-v_0^2=2ax\)
• finding distance: \(x=v_0t+\frac 12at^2,x=(v_0+v_f)t/2\)

Projectile Motion

In projectile motion, the horizontal motion and the vertical motion are independent of each other; that is, neither motion affects the other. When we analyze these problems, we try to separate the \(x\) and \(y\) components, set the equations up, solve them separately and combine our answers.

Here are some useful formulas to memorize, but make sure you do know how to derive them! However, what usually matters more is how well you understand them instead of memorization.

Time of flight

\[ t=\dfrac{2v_0\sin\theta}g \]

Maximum height reached

\[ y_{max}=\dfrac{v_0^2\sin^2\theta}{2g} \]

Horizontal range

\[ R=\dfrac{v_0^2\sin(2\theta)}{g} \]

Derivation

Let the projectile be launched with an initial velocity \(v_0\) at angle \(\theta\) with respect to the horizontal surface, then its \(x\) and \(y\) components will be:

\[ v_{0x}=v_0\cos\theta,v_{0y}=v_0\sin\theta \]

The object reaches the highest point when its \(v_y\) gets to zero. Thus:

\[ t=v_{0y}/g,y_{max}=v_{0y}t-\frac12gt^2=\frac{v_{0y}^2}{2g}=\dfrac{v_0^2\sin^2\theta}{2g} \]

When reaching the farthest point in \(x\) direction, the object falls on the ground, by symmetry we know that this process takes twice the time of reaching the highest point, so:

\[ R=v_{0x}\times 2t=\frac{2v_{0x}v_{0y}}{g}=\frac{v_0^2\times 2\cos\theta\sin\theta}{g}=\frac{v_0^2\sin(2\theta)}{g} \]

The last step is done with double angle formula \(2\cos\theta\sin\theta =\sin(2\theta)\) .

When we are throwing an object up to a ramp with angle \(\phi\), things will be more complicated. In this case, we can think of the projectile motion as a quadratic function and solve for the intersection. An alternative solution would be shifting the axis of our plane so that the \(x\) axis is the ramp and \(y\) axis perpendicular to it.

Forces and Newton's Laws

Common forces that you need to consider in your free body diagram:

• Gravitational force \(mg\)
• Spring force \(-kx\)
• Centripetal force \(mv^2/r\)
• normal force \(N\)
• friction force \(f\le \mu N\) opposes the motion of the body

Some common models that you want to be familiar with:

• inclined plane：\(N=mg\sin\theta,f=\mu N,F_x=mg\cos\theta-\mu mg\sin\theta\)
• rolling without slipping \(v=\omega r\)
• tension \(T\) is always along the direction of rope

We can focus on these relations to set up our equations:

• force balance \(F_{net}=ma\)
• torque balance \(\tau = I\alpha\)
• Conservation of momentum & angular momentum & energy

If the system consists of mass points \(m_i\):

• coordinate of center of mass \(\vec{r_c}=\sum m_i\vec{r_i}/\sum m_j\)
• total momentum \(\vec{P}=\sum m_i\vec{v_i}\)
• total angular momentum \(\vec{L}=\sum m_i\vec{r_i}\times \vec{v_i}\)
• kinetic energy \(K=\sum m_iv_i^2/2\)

In the frame \(S'\) where the mass center's velocity is \(\vec{v_c}\):

\[\vec{L}=\vec{L_c}+M\sum \vec{r_c}\times\vec{v_c},K=K_c+\dfrac12Mv_c^2,\vec{P}=\vec{P_c}+M\vec{v_c}\]

Elastic Collision

For two objects with initial velocity \(v_1,v_2\) and mass \(m_1,m_2\), after elastic collision their mass.

\[ v_1'=\dfrac{m_1-m_2}{m_1+m_2}v_1+\dfrac{2m_2}{m_1+m_2}v_2 \]

Derivation

By conservation of momentum, our center of mass moves at a constant velocity:

\[ v_c=\frac{m_1v_1+m_2v_2}{m_1+m_2} \]

We will work at the frame of reference where the center of mass is at rest. In this frame, our total momentum is zero! Thus \(p_1'+p_2'=p_1+p_2=0\). By conservation of energy, we also have:

\[ \frac12m_1v_1'^2+\frac12m_2v_2'^2=\frac{p_1'^2}{2m_1}+\frac{p_2'^2}{2m_2}=\frac{p_1^2}{2m_1}+\frac{p_2^2}{2m_2} \]

Plug in \(p_1'=-p_2'\), it's not hard to see for this quadratic equation, the other solution have to be \(p_1'=-p_1=p_2\) . Thus, in this frame we have

\[ v_1'=\dfrac{p_1'}{m_1}=\dfrac{m_2(v_2-v_c)}{m_1}=\dfrac{m_2}{m_1}\dfrac{m_1(v_2-v_1)}{m_1+m_2}=\dfrac{m_2(v_2-v_1)}{m_1+m_2} \]

by velocity addition we can get mass \(1\)'s velocity in our original frame:

\[ v_1'=\dfrac{m_2(v_2-v_1)}{m_1+m_2}+\frac{m_1v_1+m_2v_2}{m_1+m_2}=\dfrac{m_1-m_2}{m_1+m_2}v_1+\dfrac{2m_2}{m_1+m_2}v_2 \]

Work and Energy

• Work: \(W=F\cdot s=Fs\cos\theta\)
• Kinetic energy: \(E_k=\frac12mv^2=p^2/2m\)
• Gravitational potential energy: \(E_p = mgh\)
• Spring potential energy: \(U=\frac12kx^2\)

• Potential energy-force relationship: \(F=-\dfrac{dU}{dx}\)

• Work-energy theorem: \(W=\Delta K\)

• An object is at equilibrium if \(dU/dx= 0\). An equilibrium is stable if the potential energy is at local minimum, otherwise it's unstable.

Rotating Objects

• torque \(\tau=r\times F\)
• angular momentum \(L=r\times p = mvr_\theta\)
• moment of inertia \(I=\sum r^2dm\), which can be derived by hand but it's faster to remember the values:

• Parallel axis theorem: the moment of inertia about a parallel axis is the center of mass moment plus the moment of inertia of the entire object treated as a point mass at the center of mass.

\[ I=I_{cm}+Md^2 \]

• Perpendicular axis theorem: \(I_z=I_x+I_y=\int(x^2+y^2)dm\)
• rotational kinetic energy \(K_r=\dfrac12I\omega^2\)

People often get confused about rotational object, however, it's actually very similar to linear motion. We can draw comparison between these quantities:

• angle \(\theta\) to displacement \(x\)
• angular velocity \(\omega\) to velocity \(v\)
• torque \(\tau\) to force \(F\)
• angular momentum \(L\) to momentum \(p\)
• moment of inertia \(I\) to mass \(m\)
• rotational kinetic energy \(\dfrac 12 I\omega^2=\dfrac{L^2}{2I}\) to kinetic energy \(\dfrac12 mv^2=\dfrac{p^2}{2m}\)

Gravitation

\[ F=G\frac{Mm}{r^2},U(r)=-\int_\infty^r Fdr=-\frac{GMm}{r} \]

• Kepler's First Law: a planet moves around a star in an elliptical orbit
• Kepler's Second Law: a line connecting the planet and the star sweeps out equal area in equal times.
• Kepler's Third Law: square of the orbital period is proportional to cube of the semimajor axis. \(T^2\propto a^3\)

Remark: The second law is a result of conservation of angular momentum, while the other two laws requires the gravitational force to be exactly inverse proportional to square of the distance between two stars. (\(F\propto r^{-2}\))

Circular Orbit

• velocity: \(\(mv^2/R=GMm/R^2\implies v= \sqrt{GM/R}\)\)
• kinetic energy: \(\dfrac12mv^2=\dfrac{GMm}{2R}\)
• total energy: \(\dfrac 12mv^2-\dfrac{GMm}{R}= -\dfrac{GMm}{2R}\)
• angular momentum: \(L=mvR = m\sqrt{GMR}\)

Escape Velocity

By conservation of energy, we would have

\[\dfrac12mv_e^2-\dfrac{GMm}{R}=0\implies v_e=\sqrt{\dfrac{2GM}{R}}\]

Elliptical Orbit

First, we would like to prove that the orbit of a planet of mass \(m\) is indeed elliptical and the big mass \(M\) is the focus of the eclipse. (by big mass, we mean \(m\ll M\)) By Newton's second law,

\[ m\dfrac{d\vec{v}}{dt}=-\dfrac{GMm}{r^2}\hat{r} \]

Apply chain rules \(\dfrac{d\vec{v}}{dt}=\dfrac{d\vec{v}}{d\theta}\dfrac{d\theta}{dt}\) , also conservation of angular momentum tells us that \(mr^2\dfrac{d\theta}{dt}=L\). Then

\[ \dfrac{d\vec{v}}{d\theta}=-\dfrac{GMm}{L}\hat{r} \]

Define \(\hat{\theta}\) to be the unit vector perpendicular to \(\hat{r}\) pointing in the direction \(\hat{r}\) moves with increasing \(\theta\) . By some geometry, it's not hard to see that:

\[ \dfrac{d\hat{\theta}}{d\theta}=\hat{r} \]

Plug it back and we now have:

\[ \dfrac{d}{d\theta}(\vec{v}-\dfrac{GMm}{L}\hat{\theta})=0 \]

Thus, the quantity \(\vec{v}-\dfrac{GMm}{L}\hat{\theta}=\vec{u}\) is a constant independent of \(\theta\) . WLOG, assume that \(\vec{u} = u\hat{j}\) . Then:

\[ v_{\theta} =\vec{v}\cdot\hat{\theta} = \dfrac{GMm}{L}+u\cos\theta \]

Since \(\vec{L}=\vec{r}\times\vec{p}=mrv_\theta\), we can substitute and get:

\[ \dfrac{L}{mr}=\dfrac{GMm}{L}+u\cos\theta \]

Simplifying this and we can solve for \(r\) with respect to angle \(\theta\):

\[ r(\theta) = \dfrac{L^2/GMm^2}{1+(Lu/GmM)\cos\theta} \]

This is the equation for an eclipse with eccentricity \(Lu/GmM\) with the focus at the origin.

Kepler's Third Law Derivation

For an elliptical orbit with semimajor axis length \(a\) and semiminor axis length \(b\), its eccentricity \(e\) is defined as \(a^2+(ae)^2=b^2\), or \(e=\sqrt{1-(b/a)^2}\) . By geometry, we know the closest distance to the focus \(r_1=a(1-e)\) and the furthest distance \(r_2=a(1+e)\). Thus:

• \(r_1r_2=a^2(1-e^2)=b^2\)
• \(r_1+r_2=2a\)

Suppose the velocity at these two points are \(v_1,v_2\), respectively, by energy and angular momentum conservation we have:

\[mv_1r_1=mv_2r_2=L\]

\[\dfrac12mv_1^2-\dfrac{GMm}{r_1}=\dfrac12mv_2^2-\dfrac{GMm}{r_2}=E\]

Rewrite \(v_1=L/mr_1,v_2=L/mr_2\) and plug it in the second equation:

\[ \dfrac{L^2}{2m^2}(\dfrac1{r_1^2}-\dfrac{1}{r_2^2})=GM(\dfrac1{r_1}-\dfrac{1}{r_2}) \]

Simplify:

\[ \dfrac{L^2}{2m^2}=\dfrac{GM}{1/r_1+1/r_2}=\dfrac{GMr_1r_2}{r_1+r_2}=\dfrac{GMb^2}{2a} \]

Notice that \(L/2m=vr/2\) is the sweeping rate of the eclipse area in Kepler's second law and the eclipse's area is \(\pi ab\), then

\[ T^2=(\dfrac{\pi ab}{L/2m})^2=\dfrac{2(\pi ab)^2}{GMb^2/2a}=\dfrac{4\pi^2 a^3}{GM}\propto a^3 \]

Orbital Energy

Moreover, we can derive that the total energy only depends on the major axis \(a\)! To see this, we add the energy at those two points together:

\[ \begin{aligned} 2E&=\dfrac{L^2}{2m}(\dfrac{1}{r_1^2}+\dfrac{1}{r_2^2})-GMm(\dfrac1{r_1}+\dfrac{1}{r_2}) \\ &= \dfrac{GMmb^2}{2a}((\dfrac{1}{r_1}+\dfrac{1}{r_2})^2-\dfrac{2}{r_1r_2})-GMm(\dfrac1{r_1}+\dfrac{1}{r_2})\\ &= \dfrac{GMmb^2}{2a}(4a^2/b^4-2/b^2)-GMm(2a/b^2)\\ &=-\dfrac{GMm}{a}\\ \implies E&=-\dfrac{GMm}{2a}\\ \end{aligned} \]

Orbital Velocity

By energy conservation, we can get the velocity

\[v^2=GM(\dfrac{2}r-\dfrac 1a)\]

Remarks: The orbital energy is determined only by the semimajor axis, whereas the angular momentum requires us to know both the semimajor and semiminor axis.

Fluids

• Archimedes principle states that the upward buoyant force that is exerted on a body in a fluid is equal to the weight of the fluid that the body displaces. \(F_b=\rho_lVg\), where \(\rho_l\) is the density of the fluid and \(V\) is the volume of the fluid that the body displaces.
• Continuity equation: basically it means that the volume flow in equals the volume flow out in any period of time. \(\rho_1A_1v_1=\rho_2A_2v_2\). Most of the time we are dealing with incompressible liquids, so we can drop the density factor and get \(A_1v_1=A_2v_2\).
• Bernoulli equation: the energy version of continuity equation \(P_1+\dfrac12\rho v_1^2+\rho gh_1=P_2+\dfrac12\rho v_2^2+\rho gh_2\)

Oscillations

Simple harmonic motion

\[ x(t)=A\cos(\omega t+\phi) \]

Where \(t\) is the time, \(x\) is the displacement, \(\omega\) is the angular frequency, \(A\) is the amplitude, and \(\phi\) is the phase shift measured in radians. This is a solution to the differential equation in either of the following forms:

\[ \begin{aligned} a=\frac{d^2x}{dt^2}=-\omega^2x\\ x^2+\frac{v^2}{\omega^2}=A^2\\ \end{aligned} \]

The first equation is derived from Newton's second law while the second one is a result of energy conservation. They are both very important to know about.

Mass on a spring

Take the most classical example of a mass \(m\) that moves horizontally while attaching to a spring with spring constant \(k\). If the system is left at rest at the equilibrium position, then no net force is acting on the mass. Otherwise, we would have the restoring elastic force by the Hooke's law:

\[ F=-kx \]

Notice that from Newton's second law we also have \(F=ma\), then we can get:

\[ a=-\frac km x=-\omega^2x,\omega = \sqrt{\frac km} \]

An alternative way is using the conservation of energy:

\[ \frac12mv^2+\frac12kx^2=\frac12mv_0^2+\frac12kx_0^2=\text{const} \]

We can also get the angular frequency by dividing the factors of \(x^2\) by the factors of \(v^2\) in this formula.

Mass on a pendulum

Another classical example will be the simple pendulum at small angle \(\theta\ll 1\).

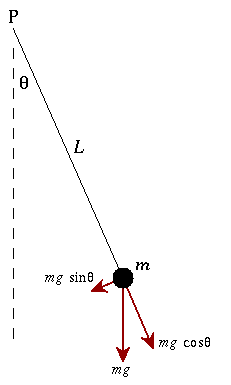
By its free body diagram we can apply Newton's second law for rotational system:

\[ \tau = I\alpha\implies -mg\sin\theta L = (mL^2)\dfrac{d^2\theta}{dt^2} \]

Plug in small angle approximation \(\sin\theta\approx \theta\):

\[ \dfrac{d^2\theta}{dt^2}+\dfrac gL\theta=0 \]

By our previous knowledge we know that the angular frequency \(\omega = \sqrt{g/L}\).

If we have a physical pendulum with moment of inertia around our pivot \(I\), then \(\omega = \sqrt{mgL/I}\) .

Below are some more formulas for some terms we use in oscillation:

• period \(T\) of an oscillation: \(T=2\pi/\omega\)
• frequency \(f\): \(f=\omega/2\pi\)

A system of \(N\) coupled oscillators has \(N\) different eigenmodes when all the oscillatros oscillate with the same frequency \(\omega_i,x_j=x_{j0}\sin(\omega_i t+\varphi_{ij})\) and \(N\) eigen-frequencies \(\omega_i\) (which can be multiple, \(\omega_i=\omega_j\)). General solution is a superposition of all the eigenmotions.

Waves

• \(v=\lambda/T=\lambda f\)
• For waves on a string, \(v=\sqrt{T/\mu}\), where \(T\) is the tension along the string and \(\mu\) is the linear density of the string.
• Doppler effect: \(f_o=\dfrac{v+v_o}{v+v_s}f_s\)